The following topics help for a better understanding of relative maxima.įAQs on Relative Maxima How Do You Find Relative Maxima?
In the food processing units, the humidity is represented by a function, and the maximum humidity at which the food is spoilt can be found using the local maxima. The voltage in an electrical appliance, at which it peaks can be identified with the help of the local maximum, of the voltage function. The price of a stock, if represented in the form of a functional equation and a graph, is helpful to find the points where the price of the stock is maximum can be found using. The maximum height reached by a ball, which has been thrown in the air and following a parabolic path, can be found by knowing the local maximum. For a parabolic equation, the local maximum helps in knowing the point at which the vertex of the parabola lies. The number of seeds to be sown in a field to get the maximum yield can be found with the help of the concept of the local maximum. Let us find some of the important applications of the relative maxima. The concept of relative maxima has numerous uses in business, economics, engineering. If the second derivative is lesser than zero \(f''(x_2)<0\), then the limiting point \((x_2)\) is the local maximum. Here x = k, is a point of local maximum, if f'(k) = 0, and f''(k) 0\), then the limiting point \((x_1)\) is the local minimum. Here we consider a function f(x) which is differentiable twice and defined on a closed interval I, and a point x= k which belongs to this closed interval (I). The second derivative test is a systematic method of finding the local maximum of a real-valued function defined on a closed or bounded interval. If the derivative of the function is positive for the neighboring point to the left, and it is negative for the neighboring point to the right, then the limiting point is the local maxima. Find one point each in the neighboring left side and the neighboring right side of the limiting point, and substitute these neighboring points in the first derivative functions. Find the first derivative of the given function, and find the limiting points by equalizing the first derivative expression to zero. The following steps are helpful to complete the first derivative test and to find the relative maxima. 
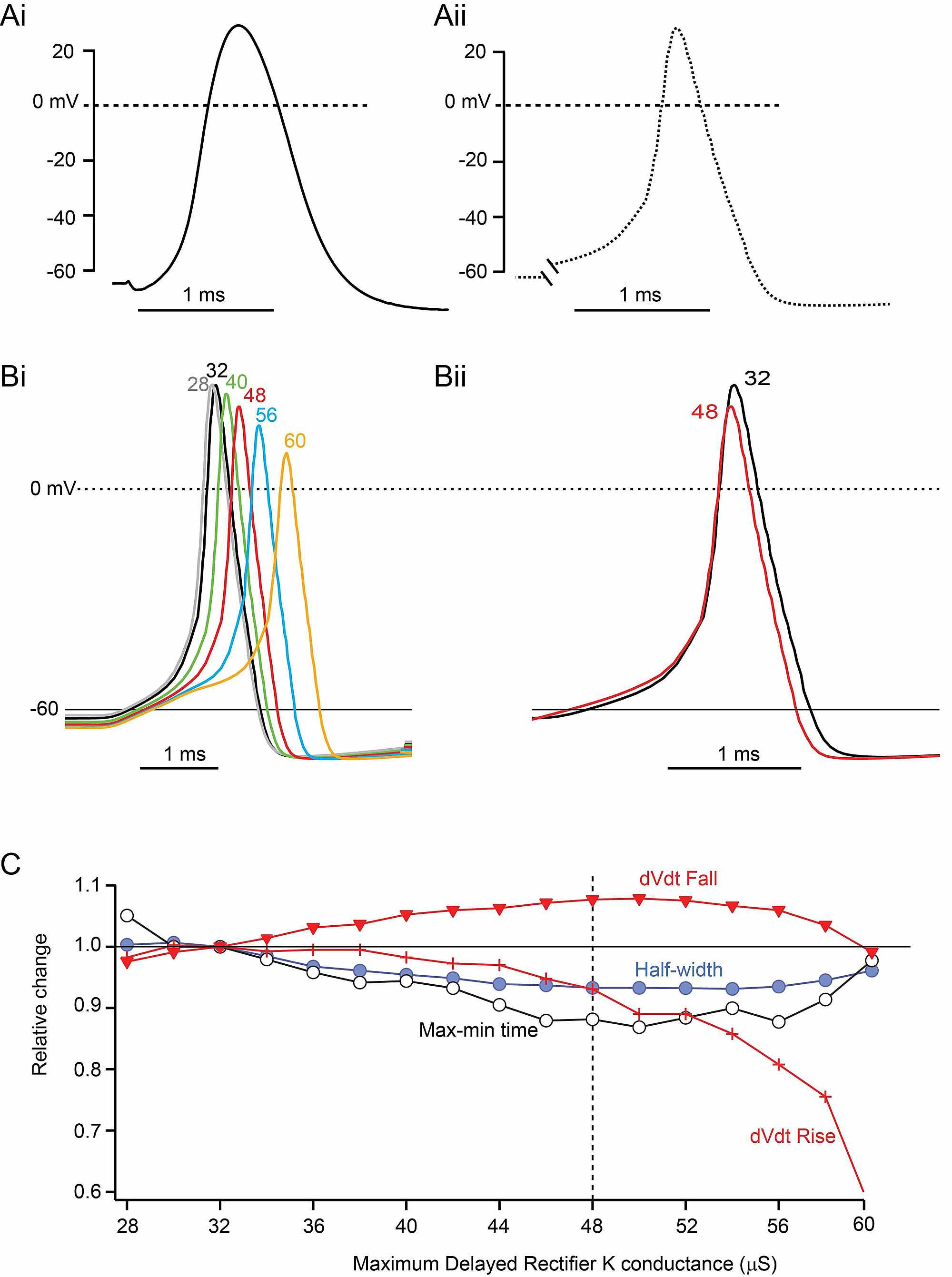
If the function values of these neighboring points are lesser than the function value at the point c, then c is the relative maxima. Also let us consider two points \(x_1\), \(x_2\) in the neighborhood of c. Here if f ′(x) changes sign from positive to negative as x increases through c. Let the function f(x) be continuous at a critical point c in the domain of the function. The first derivative test helps in finding the turning points, where the function output has a maximum value. Let us understand more details, of each of these tests. The first derivative test and the second derivative test are useful to find the relative maxima. Further the relative maxima can be identified by taking the derivative of the given function. The relative maxima can easily be found from the graph of the function, by observing the values of the neighboring points, of the relative maxima point. In addition to this, the function also has a local maximum and a global maximum. The above graph shows the relative maxima with reference to the other domain points of the function. Also, the derivative of the function is very helpful in finding the relative maxima of the function. The function equation or the graph of the function is useful to find the relative maxima. The relative maxima is the input value for which the function gives the maximum output values.
Here the point 'c' is referred as relative maxima, since its value f(c), is maximumum, in comparison with the other point values of the function. In the above graph the values of the function at the points c, \(x_1\), and \(x_2\), are f(c), \(f(x_1)\), and \(f(x_2)\) respectively. Relative Maxims is a point that is higher than the points towards its left, and towards its right. Relative maxima is a point at which the graph of the function changes direction from increasing to decreasing. It is the turning point in the graph of the function. Relative maxima can be easily identified from the graph of the function.
0 kommentar(er)
